在上篇文章中，我们确定了电力系统负荷预测对市场主体的必要性，并利用多元回归确立预测基本方法。接下来，我们将引入赤池法则和库克距离，提升负荷预测结果的精准度。

2.2曲径通幽，巧用赤池法则有效筛除弱相关要素

赤池法则（Akaike information criterion，AIC）是衡量和评价模型拟合优良性的标准，被广泛应用于权衡模型的复杂度和评价模型的拟合优良性。在日本统计学家赤池弘次首次提出该法则的论文中，模型的AIC参数以如下形式表示。其中L是最大似然函数，k表示模型回归关联的变量数目。

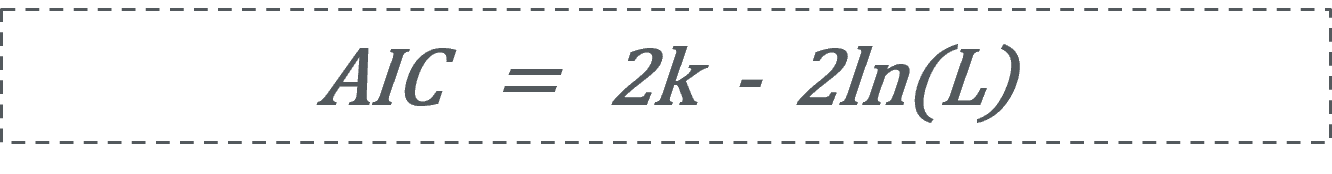
那么，这样一个“平平无奇”的式子和听起来较为抽象的最大似然函数与我们今天探讨的模型回归误差有什么关系呢？根据大数定律，当研究样本足够多时，我们可以假设模型回归的误差符合高斯分布（正态分布）。在此前提下，最大似然函数取对数（以e为底）即等价于最小平方误差，L越大意味着模型拟合精度越高。数学功底强大且看到这里不觉技痒的大神可尝试结合最大似然估计的成立条件和误差的正态分布表达式自己推导一下，而像小编一样懒于动脑的小白只需要记住这个结论就可以了。顺带一提，这个结论也是众多基于损失函数的机器学习方法的理论基础。AIC表达式可近似理解为在模型的拟合准确度-2ln(L)的基础上叠加了模型变量数目的惩罚项2k。容易看出，在过拟合情况下，模型拟合精度高但拟合所用变量较多，则L值和K值均会较大。在欠拟合的情况下，模型拟合精度差但所用变量较少，则L值和K值均会较小。两种情况下模型的AIC值均会较大。

一般而言，在回归模型考虑的变量从少变多的过程中，随着模型精度提升，似然函数L的增速会先大于k的增速，因此AIC值不断下降。但随着模型复杂度提升到了一定水平而精度增长趋缓时，似然函数L的增速逐渐小于k的增速，AIC值开始上升。因此，对于若干个不同变量数目的同类回归模型，可以优先考虑AIC值最小的模型，保证模型既具备较高适用性的同时不失预测精确度。

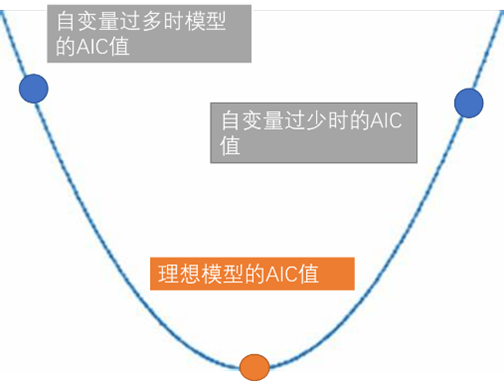
随着自变量逐步减少，AIC值呈现“先减后增”的规律

为了降低模型的复杂度，避免“维数灾”，我们根据回归模型的AIC参数去筛选关键变量，从第二阶段的回归模型出发，设计了一套精简变量的方法，具体如下：1、将所有的自变量，包括历史负荷和温度、风力、湿度和天气条件等天气信息做最小二乘法拟合，基于N个变量得到初始模型A-0（即Case2），计算A-0的AIC值AIC1；2、在A-0的基础上逐个删除变量并做最小二乘拟合，得到N个N-1个变量的模型，分别计算这些模型的AIC值，选取AIC值最小的模型作为局部最优模型A-1；3、对模型A-1重复步骤2的过程，直到某一步的局部最优模型的AIC值较上一步不再明显下降。

上述方法可以求得理论上AIC值最低的模型。但值得注意的是若起始纳入考虑拟合的变量过多，有时AIC值最低的模型仍拥有较多变量。因此在实际应用中不必墨守理论最优模型方法，可在第3步后继续结合AIC值最低点后上升的速度和模型复杂度的下降程度选取AIC值较低而拟合变量较少的模型。

基于AIC筛选弱相关变量后模型拟合效果初步提升（Case4）

我们在研究系统负荷与天气的相关性的案例中采取了上述方法，成功筛选出了对负荷影响最大的气象要素（最高温度，最低温度和天气状况）。而且在我们的案例中，仅采用关键要素去做拟合（Case 3）时模型精度要优于将全部天气信息一股脑灌进回归模型（Case 2）内。这是因为某些与负荷弱相关的变量在某些样本里波动性很大（如沿海城市海区的风力水平受受洋流和气压带影响，天与天之间波动频繁且时间分布差异较大，但海上风力在正常范围内时对城市负荷几乎无显著影响），从而放大了样本的方差，造成拟合效果偏差。确定了和负荷相关的强相关因素后，为了进一步提升模型的精度，我们尝试加入了更多城市的关键气象信息（Case 4），然而尽管模型变得更加复杂，但精确度提升效果却着实令人失望。这说明了除了气象因素和历史负荷外，仍有其他关键要素对负荷有较大的影响性。然而，由于这些要素是未知的，我们难以直接提出明确的方法来识别这些要素。因此，我们退而求其次，参考了一些聚类算法的思想，设法筛选要素含量丰富的样本，再根据这些样本的特征进行分析。

2.3一石二鸟，分析库克距离查异常指明路

距离常用于衡量样本之间的差异。在线性回归中，库克距离(Cook's Distance)描述了单个样本对整个回归模型的影响程度。某个样本的库克距离定义为基于所有样本得到的所有估计值和未包含该样本所得的估计值之间的平均差异。库克距离测量了每个样本对回归结果的影响。距离值越大则说明该样本对拟合效果的影响越大。库克距离也可以用来检测异常点。在最理想的情况下，每个样本对模型的影响是相等的。如某个样本的库克距离非常大，我们可以视这个样本为与整体特性相异的异常点。

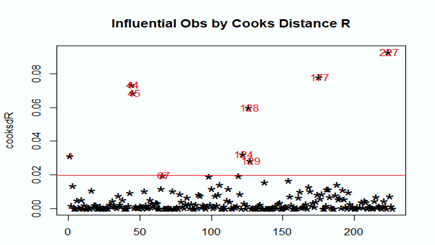
研究样本库克距离统计示意

通过反复研究数据特征，我们在本次研究中将4倍于平均距离的样本作为异常点筛选出来。剔除了这些异常样本后剩余样本总体整体特征和数量仍较为可观比较一致，大幅提升了拟合效果（Case 5）。Case 5 的拟合误差已经达到了0.9347，意味着对于特性与样本特征相近的运行日系统运行负荷预测已达较高的准确度。

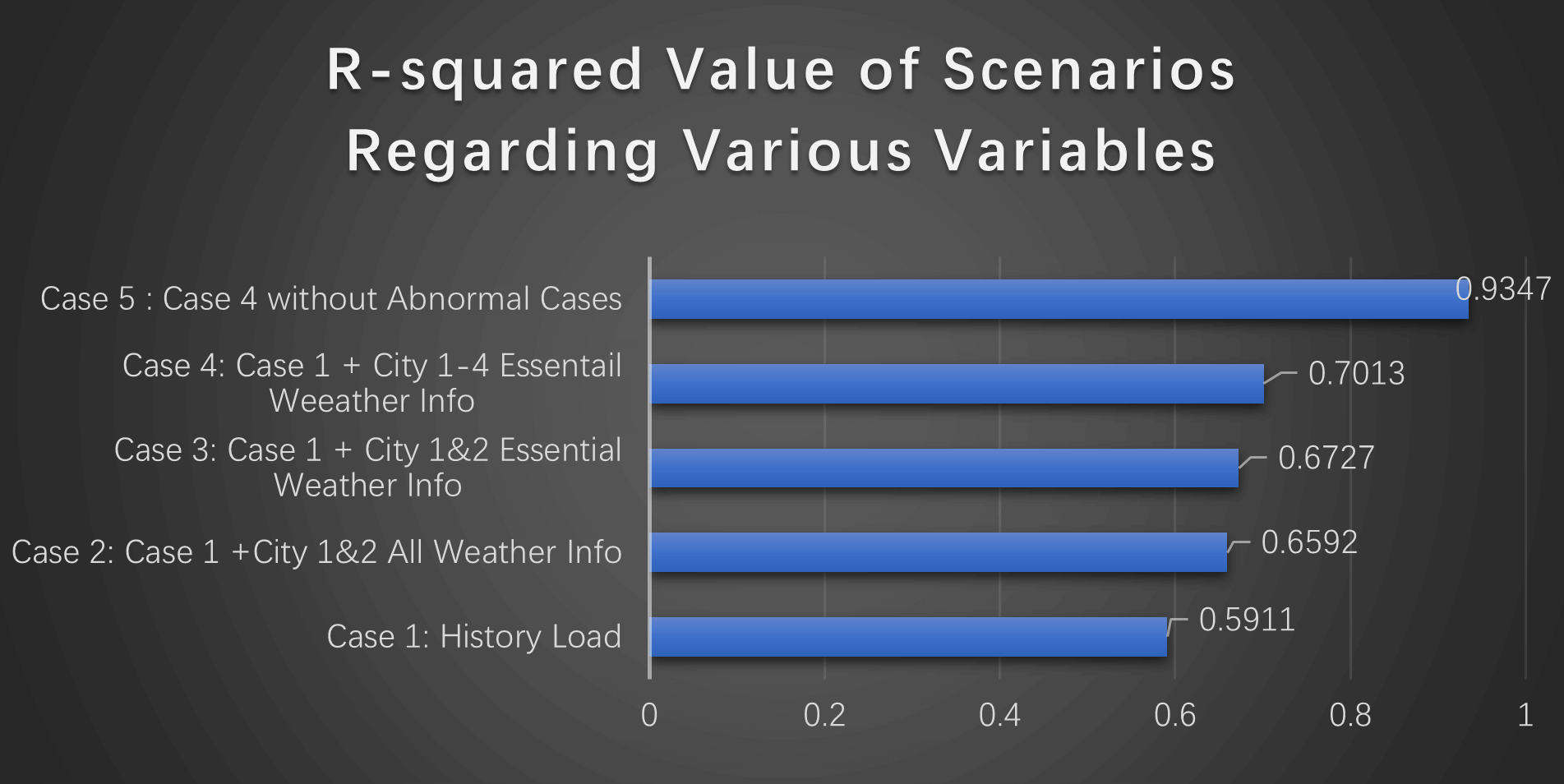
AIC+库克距离分析后模型拟合效果显著提升（Case5）

此外，我们还尝试从库克距离分析的结果进行事后分析以寻找对负荷产生显著影响的隐藏因素，从而确定模型的适用范围。通过对被筛选出来的运行日样本进行了进一步的共性特征分析，我们发现这些“异常运行日”通常分布于法定节假日结束后的工作日、强对流天气影响日以及天气状况剧烈变化约前后两天等具有某些特征的时期。对这些异常样本的分析有效加深了我们对系统负荷影响因素的进一步理解，并能在实际负荷预测中意识到模型的适用范围，有效降低预测失误率。

3小结

为了帮助市场主体有效分析市场形势，万里扬能源科技技术团队针对电力系统负荷预测开展了研究工作。我们旨在删繁就简，为市场用户设计便于应用、易于执行、复制并可自主发挥的研究手段。在本文所述的研究案例中，成功建立了“线性回归模型+赤池法则筛选弱相关变量+库克距离分析筛除异常样本”的基本分析方法。所用数据均基于公有信息，且取得了较好的拟合效果。此外，这套方法易于复制，其中的回归、筛选等方式均可替换为其他算法以进一步提升模型的准确度和适应范围，唯一要注意的是算法之间的协调配合关系。

本次研究的过程也大大启发了我们的思路，在后续样本聚类分析、归因分析和多时间尺度精细化模型应用等层面取得了一定进展，并在实战中获得了不错的效果，有效支持了我们后续开展市场中长期的研究分析工作。我们也衷心希望能耐心看到这里的看官对我们的研究进行拓展，并渴望能一起合作碰撞出更棒的成果。