本文以电力系统负荷预测为切入点，从市场主体实用的角度出发探讨系统负荷预测的基本研究思路，并提出了一套具体方法供读者参考。

1电力系统负荷预测对市场主体的必要性 

电力系统负荷作为影响价格的强相关影响因素，对市场主体进行中长期交易分析有着重要参考意义。因此电力系统负荷预测作为辅助决策依据，能在一定程度上指导电力交易员规避交易风险，帮助市场主体客观分析市场形势。因此，在用户负荷特性的研究之外，我们针对电力系统负荷预测也开展了一定的研究。然而在与市场主体的交流和调研中我们发现：由于缺乏完备的数据来源，某些在电力系统运行中有着广泛应用的数据算法无法直接迁移。此外作为交易判断依据，市场主体普遍希望预测算法能具备一定的解释性。同时预测方法总体应从简，便于市场主体进行调整或拓展。

综上，我们将研究目标定位为设计市场主体既能便于直接应用，又可拓展研究的系统负荷预测方法。目前先以短期负荷预测为切入，逐渐推广至中长期分析，希望能帮助市场主体更好地适应市场变化，规避风险。

本文以讲解预测思路和方法为主，摘录了万里扬能源科技研究团队近期发表的负荷预测技术研究主题相关论文（EI检索）部分内容，以沿海某省运行日系统负荷预测为例，展示了团队如何一步步将预测算法精度和实用性提高的过程。本文在阐述的过程中不可避免引入部分公式，但均有简单的示意和解释。希望读者朋友能各取所需，有钻研精神的大神可深入研究公式背后的含义，像小编一样懒于动脑但又想了解专业研究内容的朋友也必过度费神，遇到一时看不懂的地方也不必焦虑，可以先行收藏，需要用时再翻出来斟酌。

2.1删繁就简，利用多元回归确立预测基本方法

电力系统负荷预测是电力系统运行安排的必需支撑，也有许多成熟的相关研究和应用方法，如考虑负荷近期变化趋势的时间序列分析法、负荷求导法，考虑负荷关联因素的回归、参数估计或神经网络，考虑负荷分类特征的灰度预测法、多种距离聚类算法以及考虑实际运行经验的相似日法、负荷成因分析法等。然而上述大部分负荷预测方法大多需要电网运行数据或调度运行经验的支撑，并不可完全套用于市场主体。实际上市场主体对系统负荷预测的需求也与电网运行部门有所差异。

我们通过相关前期调研和探讨，认为适用于市场主体的系统负荷方法应具备下列几个特征：1、预测方法需完全基于市场公有信息和公布数据。由于市场主体无法掌握全面的电网运行数据，因此某些在电网运行负荷预测中表现优良的数据模型或算法反而在市场主体侧难以直接移植或套用，不得不面临“巧妇难为无米之炊”的困境。因此作为交易决策的辅助手段，市场主体适用的预测方法应完全基于市场公有信息和数据开展；2、预测方法的可解释性强。便于在实用中进行复盘修正，根据实际信息和预测经验不断提高预测精确度；3、预测方法允许一定的误差，但需保证复杂性低，收敛性好，计算资源要求低。避免交易员在交易分析时花费过多的精力在调整参数、调通数据模型和分析因果等事项。

综上，我们在研究负荷预测时优先考虑使用回归模型。本文以多元线性回归作为基本方法为例，通过对沿海某省近一年的工作日历史负荷进行回归分析。

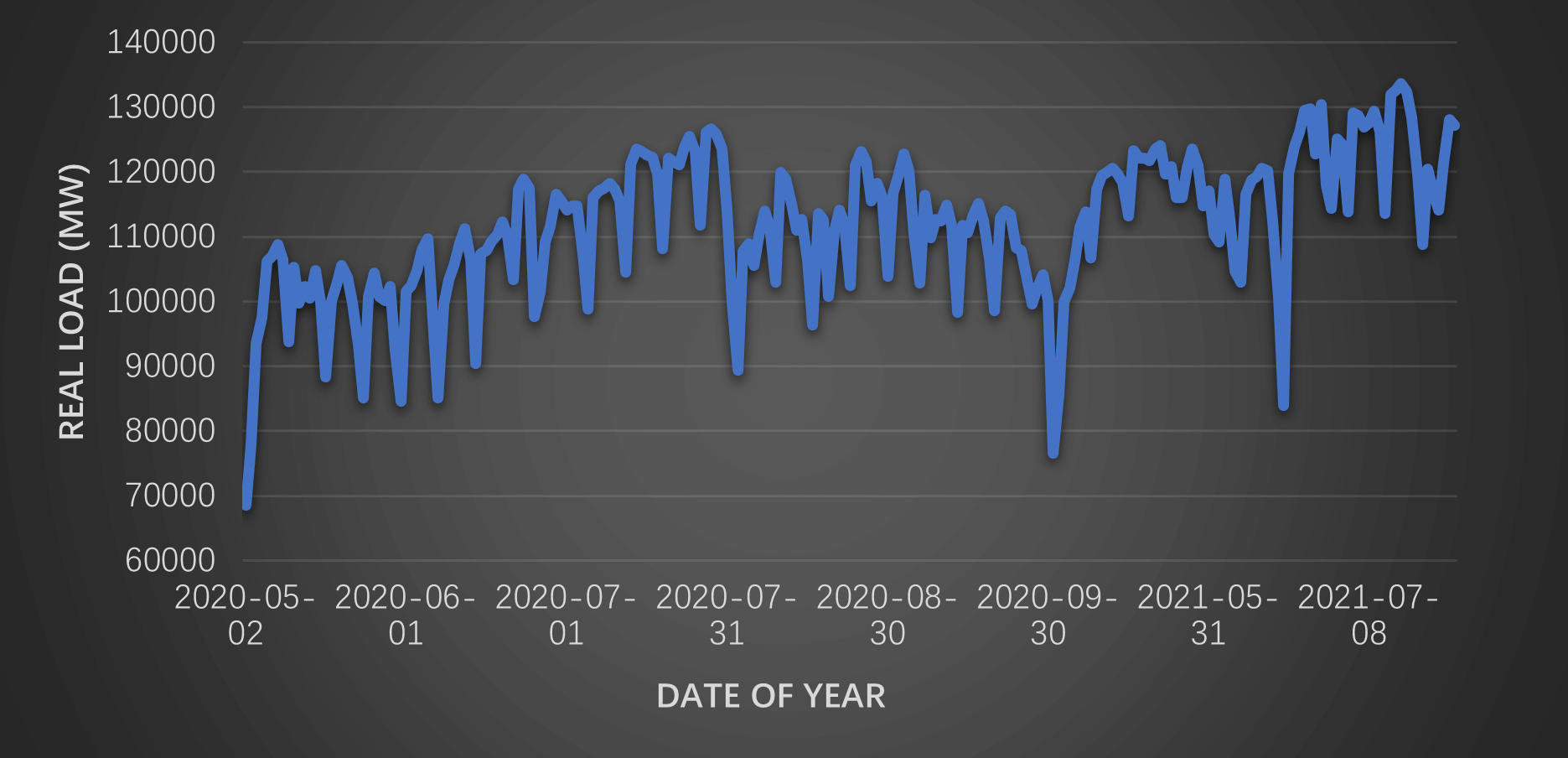
研究案例省份近年历史负荷数据示意

由于电力负荷在时间上具有一定的惯性，我们首先尝试以历史负荷作为回归变量进行预测。首先，考虑了该省市场实际负荷较运行日日前负荷信息的发布时延，简单粗暴地以目标日和目标日前两个同类型日（考虑市场公有信息发布延时）建立了线性回归模型。表达式如下所示：

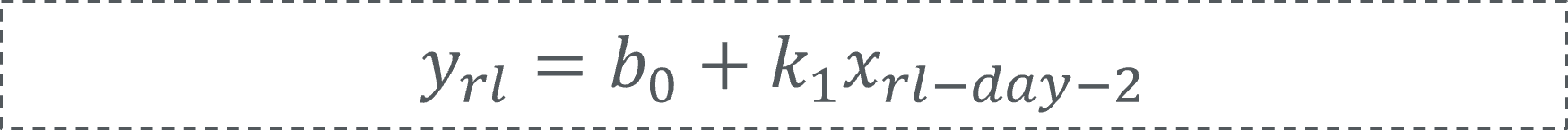
其中，xrl-day-2代表了运行日D-2天的实时系统负荷，yrl代表模型预测的运行日系统负荷。

回归模型建立后，我们采用决定系数R2来评估模型的准确度。看到这的读者朋友可能会有疑问：这个决定系数到底决定了什么呢？原来，线性回归模型中因变量的实际值可认为由两部分组成：一部分源自自变量和因变量线性关系（SSR），代表回归关系中可解释的部分。另一部分是来自自变量以外的其他无法预测因素的干扰（残差干扰（SSE）），不可用回归关系解释。为了得到较精确度线性回归模型，一般希望模型可解释的部分占比越高，无法被解释的部分占比越小。即用于拟合的自变量对因变量具有决定性的影响作用。因此定义了决定系数R2来反映因变量能通过回归关系被自变量解释的比例，即回归正确率。其表达式如下所示。

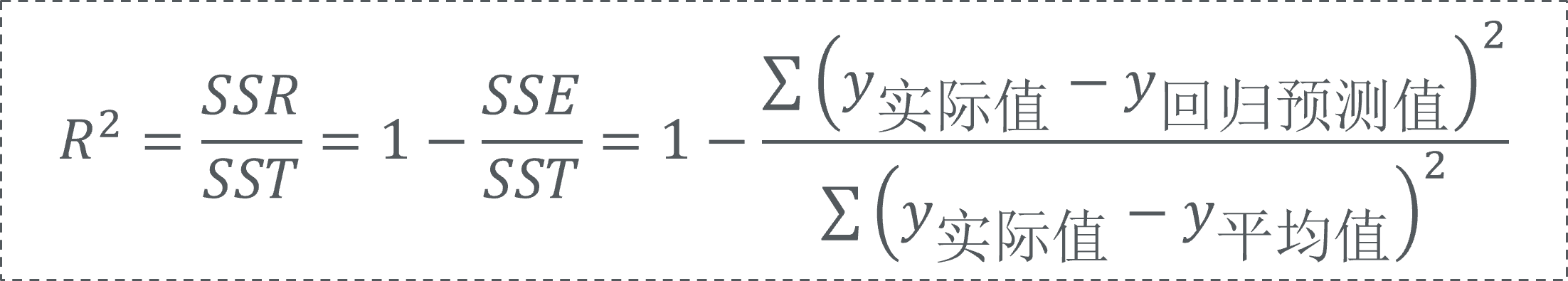
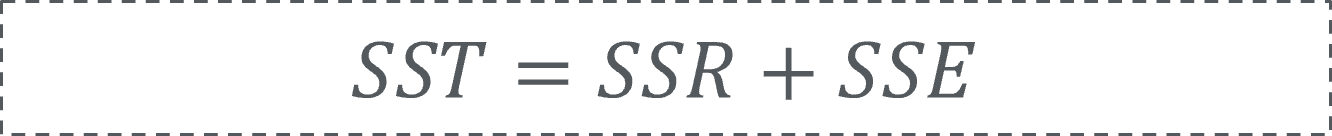
由上述表达式可见决定系数R2总是一个[0,1]区间内的值。举个例子，若R2=0.7，即意味着该回归模型的自变量和因变量间的回归关系可解释70%的因变量变化规律。因此决定系数越趋近于1，则误差越小，回归效果越好，即模型精准度越高。一般认为R2达到0.8以上则模型有较好的拟合特性。在我们的研究案例中，通过仅以历史负荷数据作为自变量进行拟合所述的线性回归模型R2的值约0.5911。可见当前模型的准确度明显不足，推测是还有未予考虑但与负荷强相关因素所致。

我们通过查阅负荷预测文献和实地调研，发现无论是学术研究还是行业生产上均认为天气条件对沿海省份的负荷影响较大。因此我们在历史负荷模型的基础上尝试加入了历史天气信息，因此形成了第二阶段的线性回归模型，希望能显著提升模型精度。

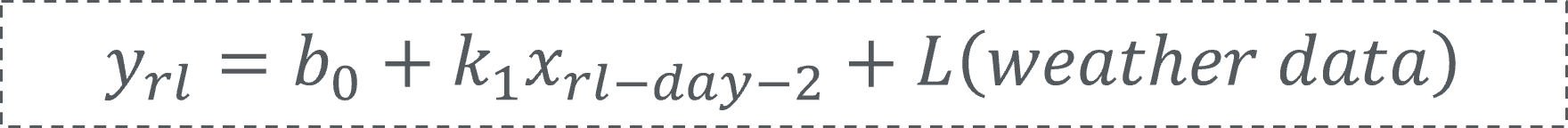
其中，L(weather data)是基于天气数据的线性组合。在这个阶段的模型里，我们加入了该省两个作为主要负荷中心的城市相关的天气数据。

这里还出现了一个有趣的情况：天气数据实际上包含着相当丰富的要素，包括但不限于最高温度、最低温度、天气状况、湿度、气压、风力和风向等。由于前期未着重对于天气条件这一要点开展充分调研，因此我们无法直观上认定哪些天气要素对负荷起到了关键的影响作用，无奈之下只好将所有天气信息都放入模型中。伴随着天气信息的不断丰富，模型的R2值确实较之前有所上升，但却在0.65左右停滞不前。即使多加入几个城市的天气信息，R2值也仅获得数个百分点的提升。我们意识到一味粗暴地加入天气信息无法进一步提升模型精度，原因是某些和负荷弱相关的因素妨碍了回归模型的有效拟合。

此外，堆砌海量的天气信息导致模型的复杂度异常大，光是维护起来也够呛。因此我们中止了加入更多参数，转而寻求有效的方法，希望能筛除与负荷相关度低的要素。

最终赤池法则脱颖而出被我们选中，该方法原理是什么，又是如何解决问题的，请在下一篇文章中一探究竟。

作者：万里扬能源科技研究院